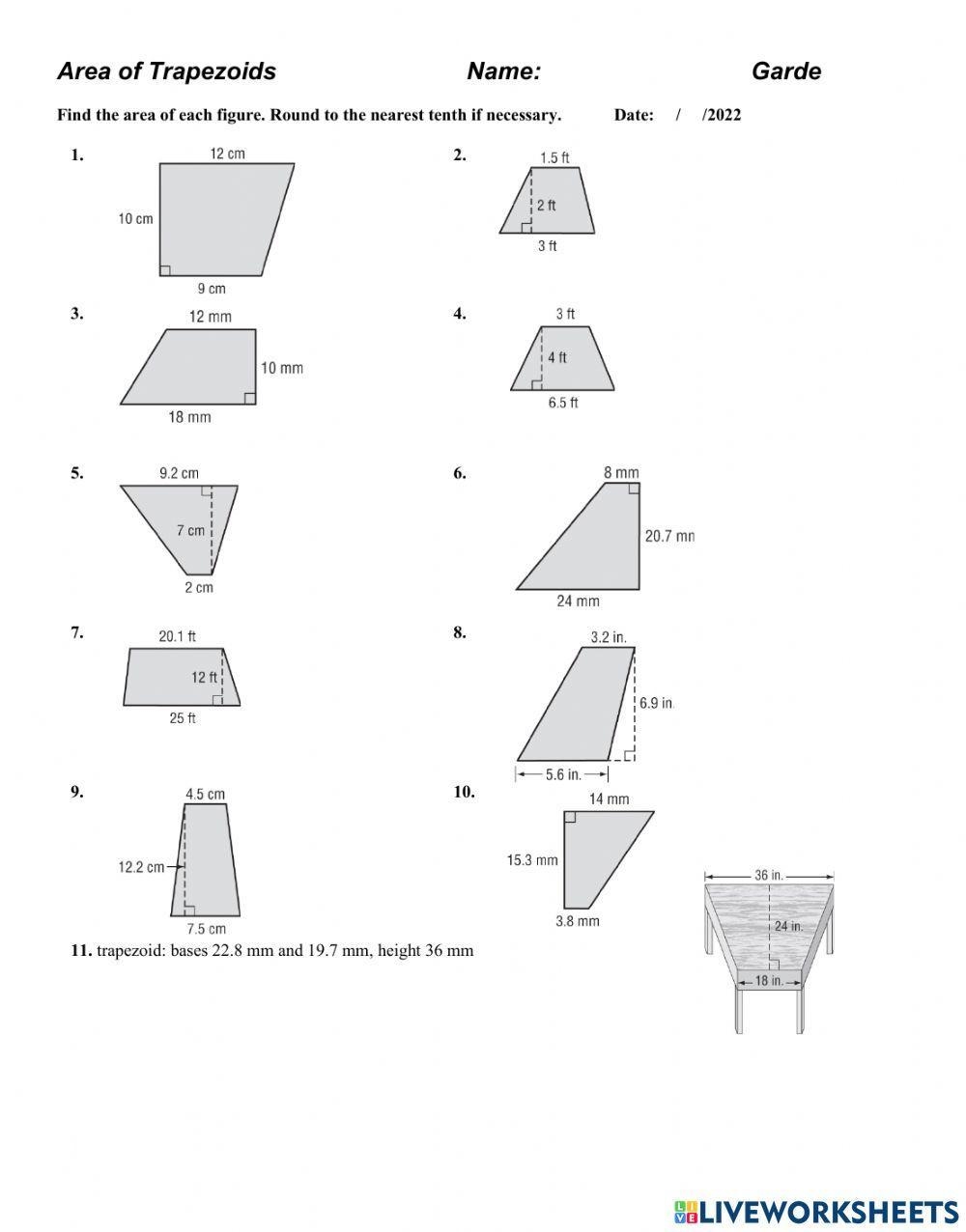
When it comes to geometry, one of the fundamental concepts that students often encounter is the area of various shapes. One such shape is the trapezoid, which is a quadrilateral with at least one pair of parallel sides. Understanding how to calculate the area of a trapezoid is essential for solving geometry problems and real-life applications. In this worksheet, we will explore the formula for finding the area of a trapezoid and provide practice problems for students to test their understanding.
Before delving into the worksheet exercises, let’s review the formula for calculating the area of a trapezoid. The formula is: A = (a + b) * h / 2, where “a” and “b” represent the lengths of the two parallel sides of the trapezoid, and “h” is the height (or perpendicular distance) between these two sides. By plugging in the values of the side lengths and height into this formula, we can easily determine the area of the trapezoid.
Now, let’s apply this formula to solve some practice problems in the worksheet. In each question, you will be given the measurements of the parallel sides and height of a trapezoid, and your task is to calculate its area. Remember to follow the order of operations (PEMDAS) while performing the calculations and pay attention to the units of measurement provided. Practice makes perfect, so don’t hesitate to attempt multiple problems to strengthen your understanding of the concept.
As you work through the worksheet problems, make sure to double-check your answers and seek assistance if you encounter any difficulties. Understanding the area of a trapezoid is not only crucial for academic success but also for applications in fields such as architecture, engineering, and construction. By mastering this concept, you will enhance your problem-solving skills and be better prepared for more advanced geometry topics.
In conclusion, the area of a trapezoid plays a significant role in geometry and real-world scenarios. By completing this worksheet and practicing the calculations, you will develop a solid grasp of how to determine the area of a trapezoid accurately. Remember to utilize the formula and apply it systematically to solve each problem. With dedication and persistence, you will become proficient in calculating the area of trapezoids and excel in geometry studies.